
Simpsonen paradoxa probabilitate eta estatistikako fenomeno bat da: hainbat datu-multzo zein bere aldetik aztertzen direnean joera bat agertzen da, baina joera hori desagertu egiten da (edo alderantzikatu) taldeak konbinatzen direnean. Fenomeno hori askotan azaltzen da gizarte-zientzien eta medikuntza-zientzien estatistiketan, eta bereziki kaltegarria da aztertutako arazoaren arrazoia zein den jakiteko maiztasun-datuak ez direnean ondo interpretatzen. Paradoxa ikuspegi estatistikoari behar bezala helduz konpon daiteke.
Adibidea:
Giltzurrun-kalkuluen tratamendua
Adibide hau benetako azterketa mediko batetik hartua da, giltzurruneko kalkuluetarako bi tratamenduren arrakasta-tasak alderatzen ditu. Taulak tratamendu horien arrakasta-tasak erakusten ditu: ehunekoak eta kopuru zehatzak ematen ditu, eta kalkulu txikien tratamenduak eta kalkulu handienak bereizten. A tratamenduak prozedura kirurgiko irekiak eta B tratamenduak prozedura kirurgiko itxiak hartzen ditu barne. Parentesi arteko zenbakiek taldearen guztizko tamainarekiko arrakasta-kasuen kopurua adierazten dute.
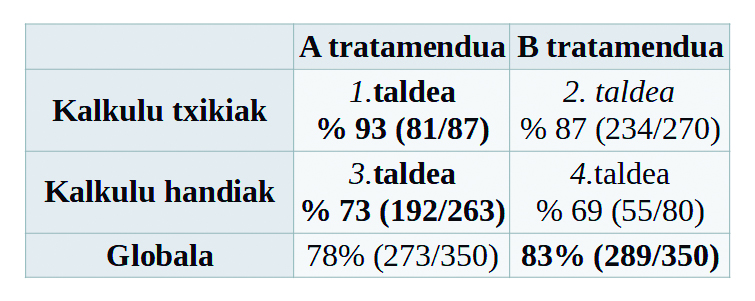
A tratamenduak prozedura kirurgiko irekiak eta B tratamenduak prozedura kirurgiko itxiak barne hartzen ditu. Parentesi arteko zenbakiek taldearen guztizko tamainarekiko arrakasta-kasuen kopurua adierazten dute. Ondorio paradoxikoa da A tratamendua eraginkorragoa dela kalkulu txikietan zein handietan erabiltzen denean, nahiz eta B tratamendua eraginkorragoa den bi tamaina horiek aldi berean hartzen direnean. Kasu honetan, ez zekiten «ezkutuko» aldagaia (edo nahasmen-faktorea), «kalkuluaren tamaina», garrantzitsua zenik haren ondorioak aztertu zituzten arte.

